01 Matrix

Problem statement

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

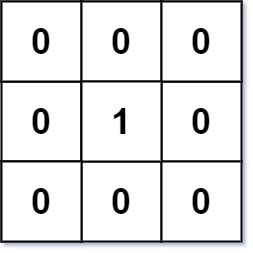
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

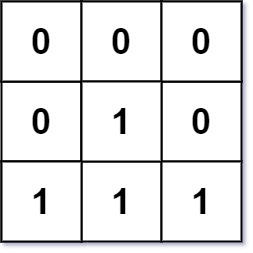
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

My solution

/**
 * @param {number[][]} mat
 * @return {number[][]}
 */
var updateMatrix = function(mat) {
    scanFromLeft(mat)
    scanFromRight(mat)
    
    return mat;
};

function scanFromRight(mat) {
    const rows = mat.length;
    const columns = mat[0].length;
    
    for (let i = rows - 1; i >= 0; i--) {
        for (let j = columns - 1; j >= 0; j--) {
            if (mat[i][j] > 0) {
                if (i + 1 < rows) {
                    mat[i][j] = Math.min(mat[i][j], mat[i + 1][j] + 1)
                }
                
                if (j + 1 < columns) {
                    mat[i][j] = Math.min(mat[i][j], mat[i][j + 1] + 1)
                }
            }
        }
    }
}

function scanFromLeft(mat) {
    const rows = mat.length;
    const columns = mat[0].length;
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < columns; j++) {
            if (mat[i][j] > 0) {
                mat[i][j] = Number.MAX_SAFE_INTEGER;
                
                if (i > 0) {
                    mat[i][j] = Math.min(mat[i][j], mat[i - 1][j] + 1)
                }
                
                if (j > 0) {
                    mat[i][j] = Math.min(mat[i][j], mat[i][j - 1] + 1)
                }
            }
        }
    }
}