Convert Sorted List to Binary Search Tree

Problem statement

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

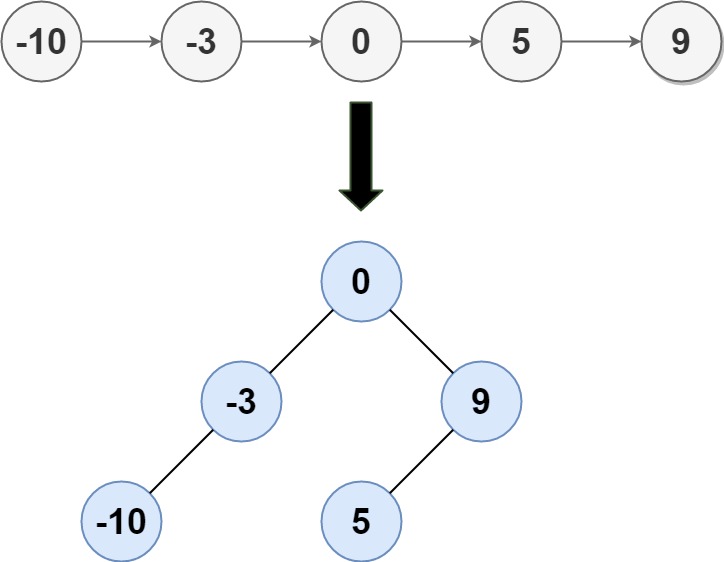
Input: head = [-10,-3,0,5,9]Output: [0,-3,9,-10,null,5]Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []Output: []

Constraints:

• The number of nodes in head is in the range [0, 2 * 104].
• -105 <= Node.val <= 105

My solution

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {ListNode} head
 * @return {TreeNode}
 */
var sortedListToBST = function(head) {
    return buildBST(head)
    
    function buildBST(head) {
        if (!head) {
            return null;
        }
        
        const median = findMedian(head)
        const root = new TreeNode(median.val)
        root.right = buildBST(median.next);
        
        let prev = findPrev(head, median);
        
        // console.log("prev", prev, root, median)
        
        if (prev) {
            prev.next = null;
            root.left = buildBST(head)
        } else {
            root.left = null
        }
        
        return root;
    }
};

function findMedian(node) {
    let fast = node;
    let slow = node;
    
    while (fast !== null) {
        // console.log("fast", fast)
        fast = fast.next;
        if (fast === null) {
            break;
        }
        fast = fast.next
        slow = slow.next
    }
    
    return slow
}


function findPrev(head, tail) {
    if (head === tail) {
        return null
    }
    let prev = head;
    while (prev.next !== tail) {
        prev = prev.next;
    }
    
    return prev;
}