Special Positions in a Binary Matrix

Problem statement

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

Example 1:

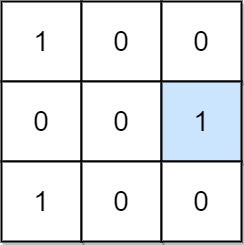
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]Output: 1Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

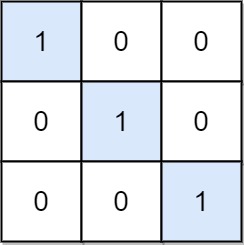
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]Output: 3Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• mat[i][j] is either 0 or 1.

My solution

/**
 * @param {number[][]} mat
 * @return {number}
 */
var numSpecial = function(mat) {
    const rowSum = mat.map(row => row.reduce((acc, curr) => acc + curr,0));
    const colSum = Array.from(new Array(mat[0].length)).fill(0);
    for (let i = 0; i < mat.length; i++) {
        for (let j = 0; j < mat[0].length; j++) {
            // console.log(mat[i][j], colSum[j], i, j)
            colSum[j] += mat[i][j];
        }
    }
    
    let count = 0;
    
    for (let i = 0; i < mat.length; i++) {
        for (let j = 0; j < mat[0].length; j++) {
            if (mat[i][j] === 1 && rowSum[i] === 1 && colSum[j] === 1) {
                count++
            }
        }
    }
    
    
    
    return count;
};